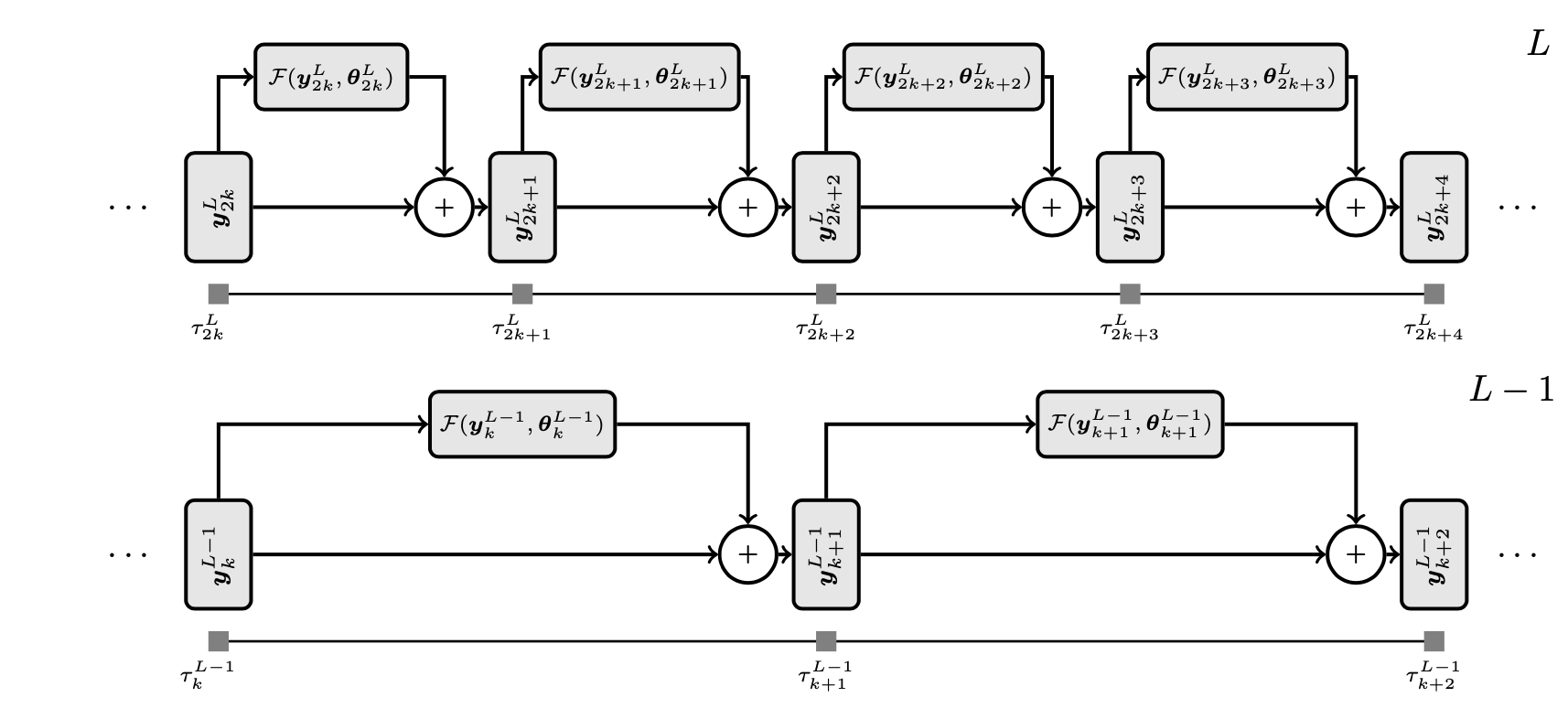
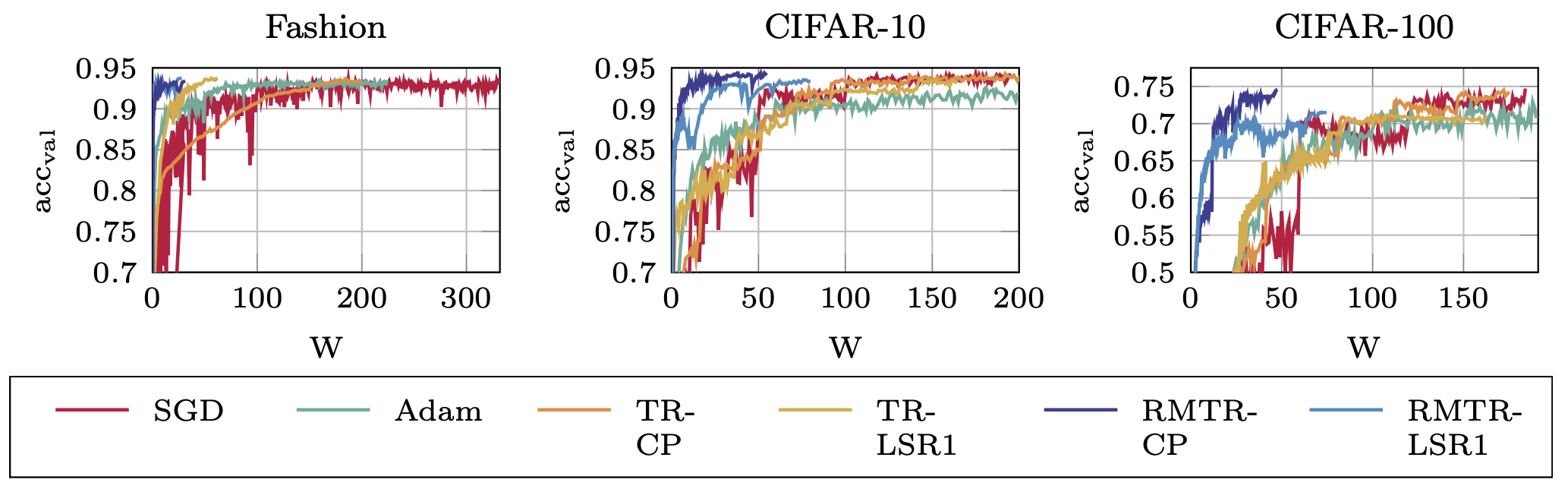
Deep neural networks (DNNs) suffer from a computationally exhaustive training phase, which limits their applicability and hinders their development. During the training phase, the parameters of the network are determined by minimizing a highly non-convex loss function. My research objective is to enhance the training of DNNs by leveraging multilevel and domain-decomposition techniques. This entails developing novel optimization methods which perform well in large-scale stochastic settings. Thus, developing methods that are memory and computationally efficient and convergence that does not deteriorate in the presence of sub-sampling noise. Moreover, it is important to devise suitable strategies for constructing a hierarchy of subspaces. This can be achieved by exploring the structure of the network's architecture, data representation, and the properties of the loss function.

Modeling and predicting the dynamics of complex multiscale and multiphysics problems is a long-standing challenge in science and engineering. Scientific Machine Learning (SciML) enables modeling complex, possibly unknown, dynamics and facilitates fast prediction by integrating data-driven and physics-informed approaches. However, despite the great promise of SciML approaches, there are still many open theoretical and practical questions related to error control, and numerical stability, which prohibit the reliable use of SciML in real-life applications. My research interest involves integrating the latest SciML approaches into current state-of-the-art large-scale solution strategies. Using such hybrid approaches offers promising research direction, as they maintain the robustness and accuracy of traditional numerical methods while harnessing the efficiency of SciML approaches.

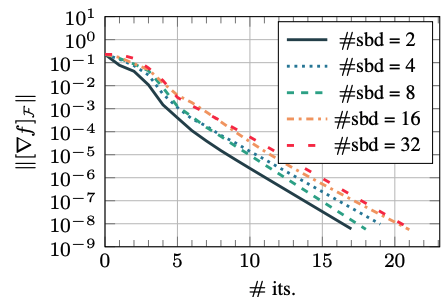
Nonlinear field-split or domain-decomposition preconditioners enable an efficient solution of large-scale nonlinear multi-physics problems. The idea behind these methods is to enhance the convergence of nonlinear solution strategies by rebalancing the nonlinearities, or by transforming the basis of the solution space. This can be achieved by decomposing either the computational domain or the physics of the coupled problems. Former is of particular interest in the field of scientific computing, as it allows for massive parallelization. My research goal is to enhance the class of nonlinear preconditioners by proposing novel algorithmic variants and by extending the applicability of existent approaches to a wider range of nonlinear problems.

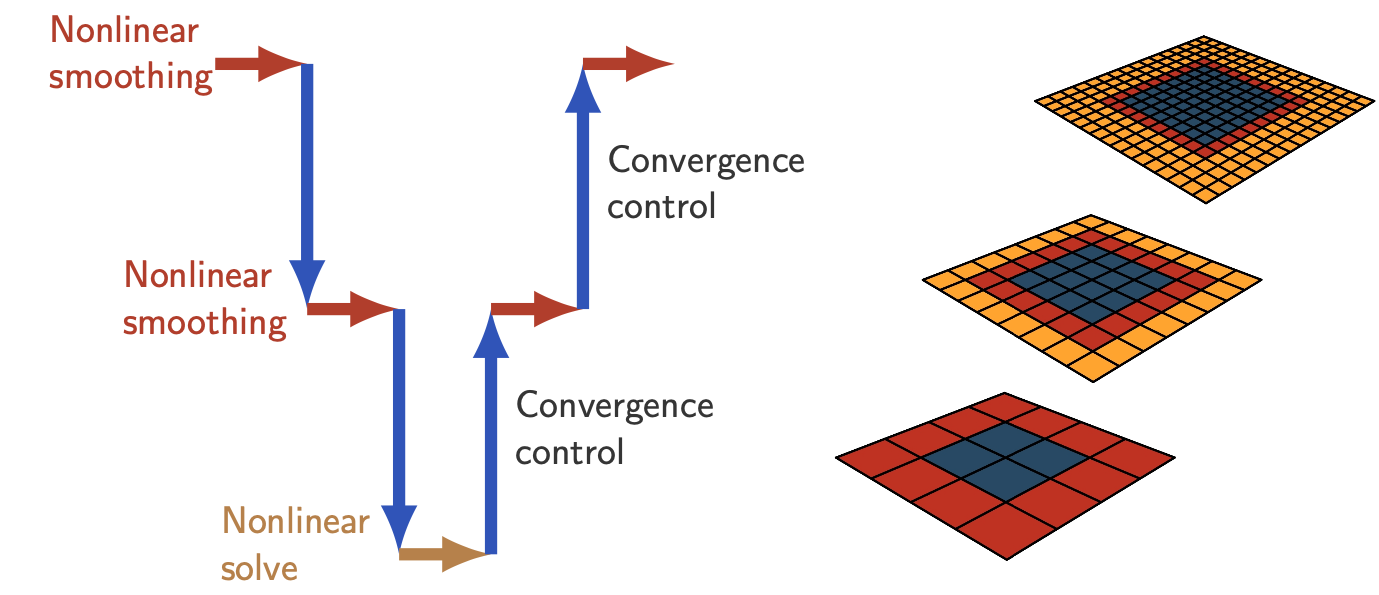
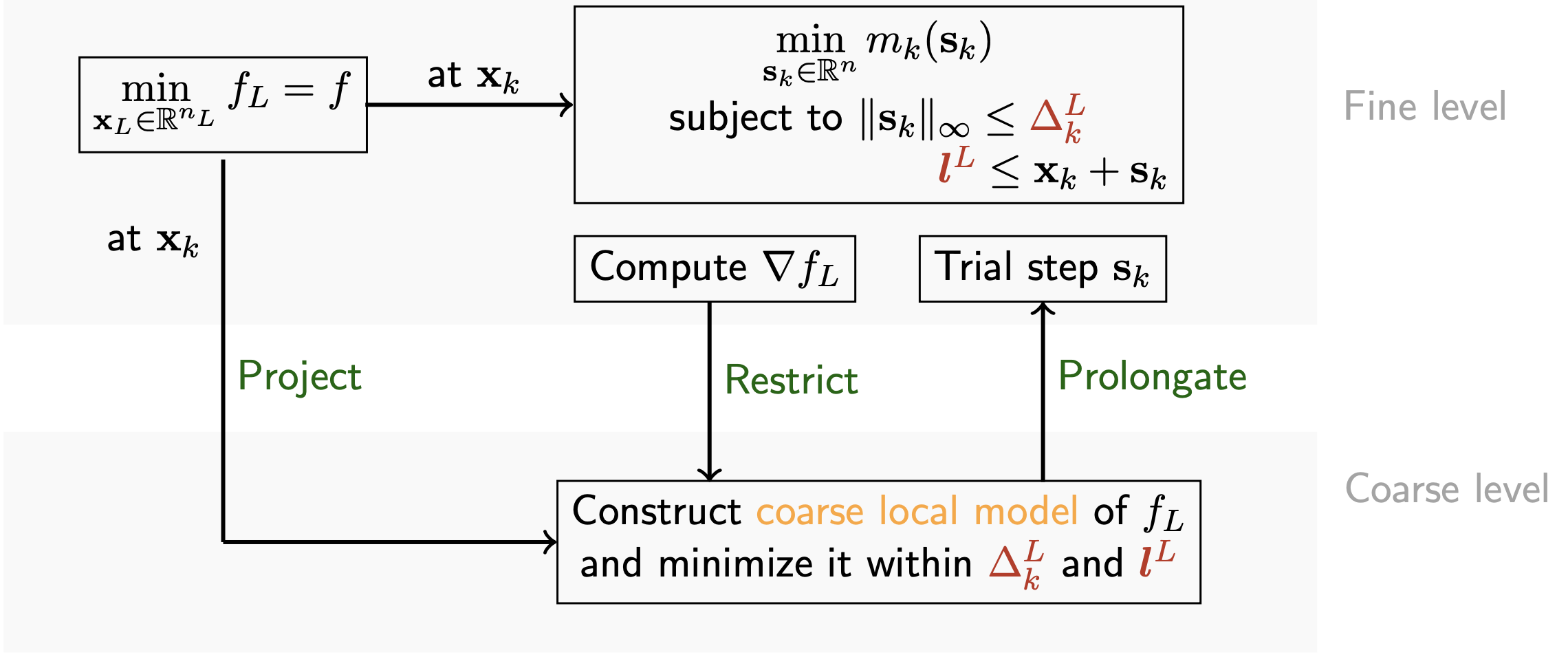
Multilevel methods were originally designed for solving elliptic partial differential equations. Their applicability to non-convex optimization problems was extended through the trust-region globalization strategy, leading to the development of recursive multilevel trust-region methods (RMTR) [Gratton et al., ’08]. I actively contribute to the development of RMTR methods by proposing several novel variants aimed at either extending applicability, improving efficiency, or enabling problem-specific optimizations. These methods are unique in that they allow for solving complex non-convex minimization problems with multigrid efficiency. Moreover, they are provably globally convergent, ensuring the success of the nonlinear iteration process.

Predicting damage and crack propagation is a long-lasting challenge in computational mechanics. The phase-field approach to fracture allows for predicting crack evolution without the need to explicitly model crack paths and therefore has become very popular. The development of an efficient phase-field fracture simulation framework requires scalable implementation of an underlying mathematical model and robust solution strategy. I have contributed to both aspects by implementing the finite-element phase-field fracture models and by proposing novel solution strategies for solving arising non-convex coupled constrained minimization problems. The developed simulation framework has been used to simulate brittle, conchoidal, and pneumatic fractures. More recently, it has been also employed for pressure-induced fracture propagation of stochastic fracture networks in 2D/3D, considering realistic scenarios with up to 1 000 fractures.

I actively contribute to the development of scientific software libraries with a particular focus on the development of large-scale, parallel nonlinear optimization strategies and simulation frameworks.